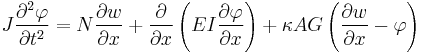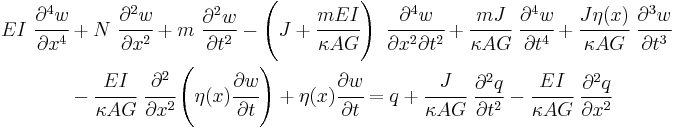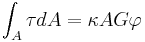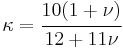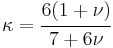Timoshenko beam theory
| Continuum mechanics |
|---|
The Timoshenko beam theory was developed by Ukrainian-born scientist Stephen Timoshenko in the beginning of the 20th century.[1][2] The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behaviour of short beams, sandwich composite beams or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam. The resulting equation is of 4th order, but unlike ordinary beam theory - i.e. Bernoulli-Euler theory - there is also a second order spatial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, while the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases.
If the shear modulus of the beam material approaches infinity - and thus the beam becomes rigid in shear - and if rotational inertia effects are neglected, Timoshenko beam theory converges towards ordinary beam theory.
Contents |
Governing equations
Quasistatic Timoshenko beam
In static Timoshenko beam theory without axial effects, the displacements of the beam are assumed to be given by
where 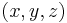 are the coordinates of a point in the beam,
are the coordinates of a point in the beam, 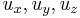 are the components of the displacement vector in the three coordinate directions,
are the components of the displacement vector in the three coordinate directions,  is the angle of rotation of the normal to the mid-surface of the beam, and
is the angle of rotation of the normal to the mid-surface of the beam, and  is the displacement of the mid-surface in the
is the displacement of the mid-surface in the  -direction.
-direction.
The governing equations are the following uncoupled system of ordinary differential equations:
The Timoshenko beam theory for the static case is equivalent to the Euler-Bernoulli theory when the last term above is neglected, an approximation that is valid when
where  is the length of the beam.
is the length of the beam.
Combining the two equations gives, for a homogeneous beam of constant cross-section,
-
Derivation of quasistatic Timoshenko beam equations From the kinematic assumptions for a Timoshenko beam, the displacements of the beam are given by Then, from the strain-displacement relations for small strains, the non-zero strains based on the Timoshenko assumptions are
Since the actual shear strain in the beam is not constant over the cross section we introduce a correction factor
 such that
such thatThe variation in the internal energy of the beam is
Define
Then
Integration by parts, and noting that because of the boundary conditions the variations are zero at the ends of the beam, leads to
The variation in the external work done on the beam by a transverse load
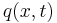 per unit length is
per unit length isThen, for a quasistatic beam, the principle of virtual work gives
The governing equations for the beam are, from the fundamental theorem of variational calculus,
For a linear elastic beam
Therefore the governing equations for the beam may be expressed as
Combining the two equations together gives
Dynamic Timoshenko beam
In Timoshenko beam theory without axial effects, the displacements of the beam are assumed to be given by
where 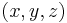 are the coordinates of a point in the beam,
are the coordinates of a point in the beam, 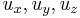 are the components of the displacement vector in the three coordinate directions,
are the components of the displacement vector in the three coordinate directions,  is the angle of rotation of the normal to the mid-surface of the beam, and
is the angle of rotation of the normal to the mid-surface of the beam, and  is the displacement of the mid-surface in the
is the displacement of the mid-surface in the  -direction.
-direction.
Starting from the above assumption, the Timoshenko beam theory, allowing for vibrations, may be described with the coupled linear partial differential equations [3]:
where the dependent variables are 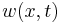 , the translational displacement of the beam, and
, the translational displacement of the beam, and 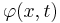 , the angular displacement. Note that unlike the Euler-Bernoulli theory, the angular deflection is another variable and not approximated by the slope of the deflection. Also,
, the angular displacement. Note that unlike the Euler-Bernoulli theory, the angular deflection is another variable and not approximated by the slope of the deflection. Also,
 is the density of the beam material (but not the linear density).
is the density of the beam material (but not the linear density). is the cross section area.
is the cross section area. is the elastic modulus.
is the elastic modulus. is the shear modulus.
is the shear modulus. is the second moment of area.
is the second moment of area. , called the Timoshenko shear coefficient, depends on the geometry. Normally,
, called the Timoshenko shear coefficient, depends on the geometry. Normally, 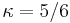 for a rectangular section.
for a rectangular section.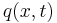 is a distributed load (force per length).
is a distributed load (force per length).
These parameters are not necessarily constants.
For a linear elastic, isotropic, homogeneous beam of constant cross-section these two equations can be combined to give [4][5]
-
Derivation of combined Timoshenko beam equation The equations governing the bending of a homogeneous Timoshenko beam of constant cross-section are From equation (1), assuming appropriate smoothness, we have
From (3), assuming appropriate smoothness,
Differentiating equation (2) gives
From equations (4) and (6)
From equations (3) and (7)
Plugging equation (5) into (8) gives
Rearrange to get
Axial effects
If the displacements of the beam are given by
where 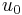 is an additional displacement in the
is an additional displacement in the  -direction, then the governing equations of a Timoshenko beam take the form
-direction, then the governing equations of a Timoshenko beam take the form
where 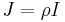 and
and 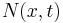 is an externally applied axial force. Any external axial force is balanced by the stress resultant
is an externally applied axial force. Any external axial force is balanced by the stress resultant
where 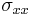 is the axial stress and the thickness of the beam has been assumed to be
is the axial stress and the thickness of the beam has been assumed to be 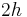 .
.
The combined beam equation with axial force effects included is
Damping
If, in addition to axial forces, we assume a damping force that is proportional to the velocity with the form
the coupled governing equations for a Timoshenko beam take the form
and the combined equation becomes
Shear coefficient
Determining the shear coefficient is not straightforward (nor are the determined values widely accepted, ie there's more than one answer), generally it must satisfy:
The shear coefficient is dependent to the Poisson's Ratio. The approaches of more precise expressions are made by many scientists, including Stephen Timoshenko, Raymond D. Mindlin, G. R. Cowper, John W. Hutchinson, etc. In engineering practices, the expressions provided by Stephen Timoshenko[6] are good enough for general cases.
For solid rectangular cross-section,
For solid circular cross-section,
See also
References
- ^ Timoshenko, S. P., 1921, On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 744.
- ^ Timoshenko, S. P., 1922, On the transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 125.
- ^ Timoshenko's Beam Equations
- ^ Thomson, W. T., 1981, Theory of Vibration with Applications
- ^ Rosinger, H. E. and Ritchie, I. G., 1977, On Timoshenko's correction for shear in vibrating isotropic beams, J. Phys. D: Appl. Phys., vol. 10, pp. 1461-1466.
- ^ Stephen Timoshenko, James M. Gere. Mechanics of Materials. Van Nostrand Reinhold Co., 1972. Pages 207.
- Stephen P. Timoshenko (1932). Schwingungsprobleme der technik. Verlag von Julius Springer.
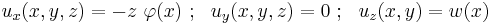
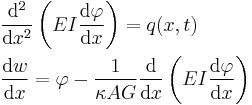
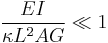
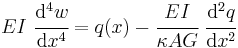
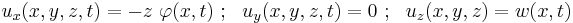
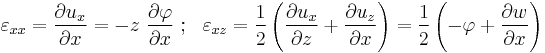
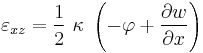
![\delta U = \int_L \int_A (\sigma_{xx}\delta\varepsilon_{xx} %2B 2\sigma_{xz}\delta\varepsilon_{xz})~\mathrm{d}A~\mathrm{d}L
= \int_L \int_A \left[-z~\sigma_{xx}\frac{\partial (\delta\varphi)}{\partial x} %2B \sigma_{xz}~\kappa\left(-\delta\varphi %2B \frac{\partial (\delta w)}{\partial x}\right)\right]~\mathrm{d}A~\mathrm{d}L](/2012-wikipedia_en_all_nopic_01_2012/I/da7aaaf2e8bd2195c72fec0a1ccddbb1.png)
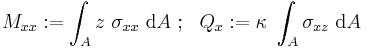
![\delta U = \int_L \left[-M_{xx}\frac{\partial (\delta\varphi)}{\partial x} %2B Q_{x}\left(-\delta\varphi %2B \frac{\partial (\delta w)}{\partial x}\right)\right]~\mathrm{d}L](/2012-wikipedia_en_all_nopic_01_2012/I/fefdaa1679c2241d6f70ea9e919c0740.png)
![\delta U = \int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \frac{\partial Q_{x}}{\partial x}~\delta w\right]~\mathrm{d}L](/2012-wikipedia_en_all_nopic_01_2012/I/ac66d562743def01b72d517bea033338.png)
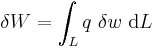
![\delta U = \delta W \implies
\int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \left(\frac{\partial Q_{x}}{\partial x} %2B q\right)~\delta w\right]~\mathrm{d}L = 0](/2012-wikipedia_en_all_nopic_01_2012/I/843257c8d66d016aa16f0df3ec8dfdf5.png)
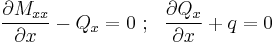
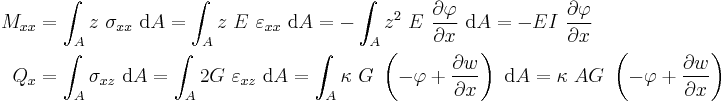
![\begin{align}
\frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) %2B \kappa AG~\left(\frac{\partial w}{\partial x}-\varphi\right) & = 0 \\
\frac{\partial }{\partial x}\left[\kappa AG\left(\frac{\partial w}{\partial x} - \varphi\right)\right] %2B q & = 0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/ed6cee8c1af34b30f1f6c9fa88a95039.png)
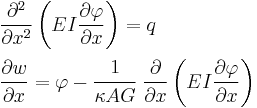
![\rho A\frac{\partial^{2}w}{\partial t^{2}} - q(x,t) = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/94525ef979901dbf2f2601ab3bba4fe7.png)
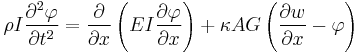
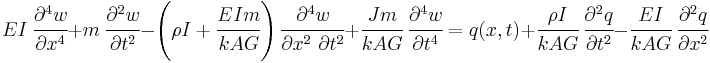
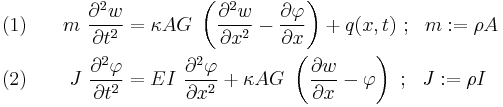
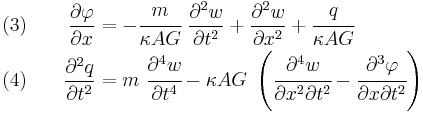
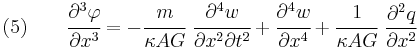
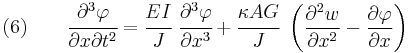
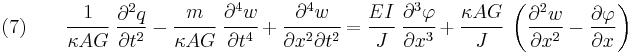
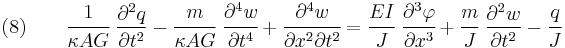
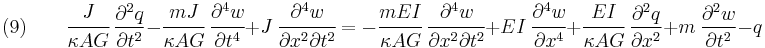
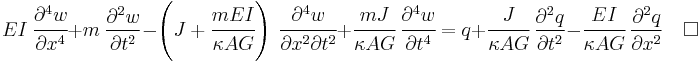
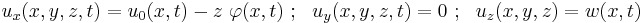
![\begin{align}
m \frac{\partial^{2}w}{\partial t^{2}} & = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] %2B q(x,t) \\
J \frac{\partial^{2}\varphi}{\partial t^{2}} & = N(x,t)~\frac{\partial w}{\partial x} %2B \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)%2B\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/e795d829b076e2e87476beeba1abc7f0.png)
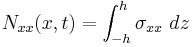
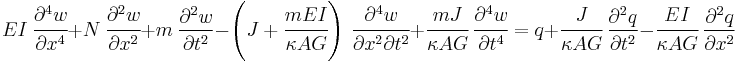
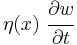
![m \frac{\partial^{2}w}{\partial t^{2}} %2B \eta(x)~\cfrac{\partial w}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] %2B q(x,t)](/2012-wikipedia_en_all_nopic_01_2012/I/f9213bee939792a798134a6284fc86d4.png)